Menu strony
Ostrosłup
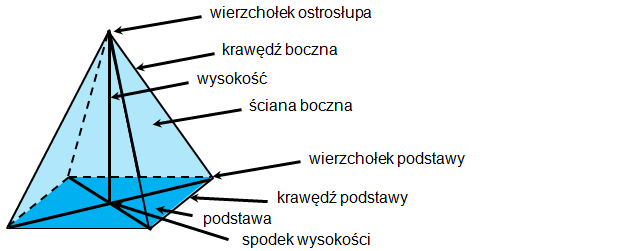
Ostrosłup – wielościan, którego wszystkie wierzchołki poza jednym leżą w jednej płaszczyźnie wyznaczając wielokąt zwany podstawą. Boki tego wielokąta nazywają się krawędziami podstawy a płaszczyzna płaszczyzną podstawy. Punkt, który leży poza płaszczyzną podstawy, nazywa się wierzchołkiem ostrosłupa, odcinki łączące go z wierzchołkami podstawy nazywają się krawędziami bocznymi. Każda krawędź podstawy wraz z wierzchołkiem ostrosłupa wyznacza trójkąt zwany ścianą boczną.Wzory

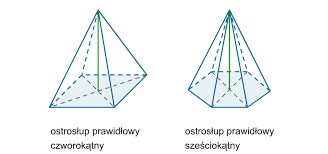
Ostrosłup prawidłowy
Ostrosłup prawidłowy (ostrosłup foremny) ma w podstawie wielokąt foremny, a spodek jego wysokości jest środkiem podstawy, tzn. jest środkiem okręgu opisanego na podstawie (jest to zarazem środek okręgu wpisanego). Ściany boczne ostrosłupa prawidłowego są przystającymi trójkątami równoramiennymi.Jeżeli spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na jego podstawie, to taki ostrosłup nazywamy ostrosłupem prostym.
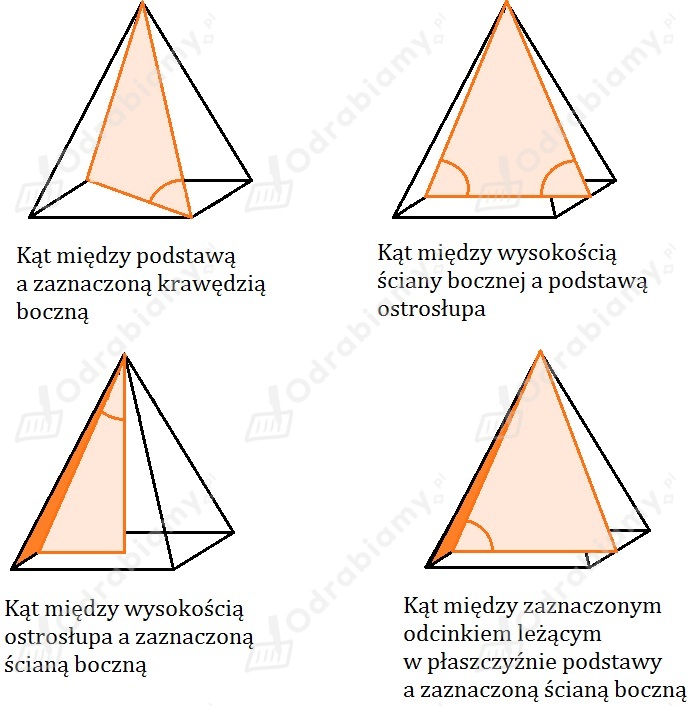
Jeśli wszystkie krawędzie boczne ostrosłupa tworzą z podstawą kąty równej miary, to spodek wysokości jest jednakowo oddalony od wierzchołków podstawy (jest więc środkiem okręgu opisanego na podstawie).
Jeśli wszystkie ściany boczne tworzą z podstawą kąty równej miary, to spodek wysokości jest jednakowo oddalony od krawędzi podstawy (jest więc środkiem okręgu wpisanego w podstawę).
Ostrosłup o podstawie n-kątnej nazywa się ostrosłupem n-kątnym (na przykład, podstawa ostrosłupa pięciokątnego jest pięciokątem).
Ostrosłup trójkątny jest inaczej nazywany czworościanem.
Ostrosłup prawidłowy czworokątny, którego podstawą jest kwadrat bywa czasem nazywany piramidą (taki bowiem kształt miały piramidy egipskie).
Przekroje ostrosłupa
Czworościan

Czworościan foremny jest przykładem trójwymiarowego sympleksu. Czworościan foremny jest dualny do samego siebie.
Czworościan foremny może być wpisany w sześcian na dwa sposoby tak, aby każdy jego wierzchołek pokrywał się z jakimś wierzchołkiem sześcianu, a każda jego krawędź z przekątną jednej ze ścian sześcianu. Objętość każdego z tych czworościanów wynosi 1/3 objętości sześcianu. Suma mnogościowa tych dwóch czworościanów tworzy wielościan zwany stella octangula, a ich część wspólna tworzy ośmiościan foremny.
Czworościany foremne wraz z ośmiościanami foremnymi wystarczą do wypełnienia całej przestrzeni. Ścinając wszystkie wierzchołki czworościanu w 1/3 długości krawędzi, uzyskujemy wielościan półforemny o nazwie czworościan ścięty.
Stopka2020 © Janusz Wachowicz. Nauczyciel matematyki i informatyki, doradca zawodowy, inżynier ogrodnik, zapraszam do współpracy! januwachi@poczta.onet.pl