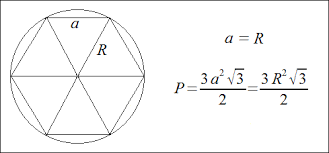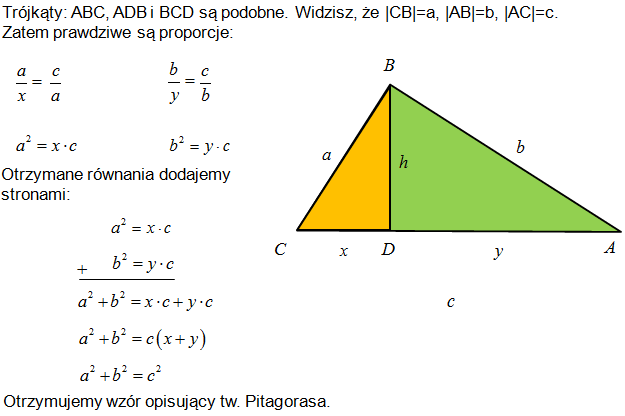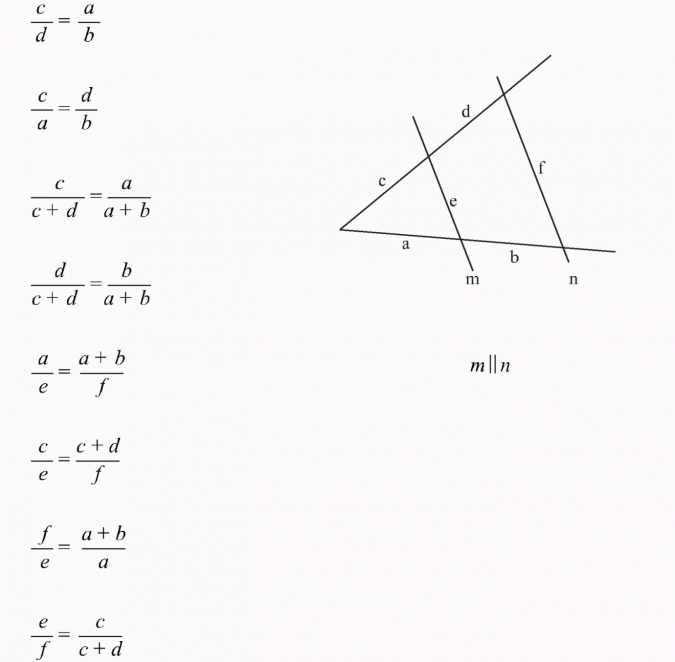Czworokąty
Czworokąt – wielokąt płaski o czterechbokach. Odcinek łączący dwa niesąsiednie wierzchołki czworokąta nazywamy przekątną czworokąta. Każdy czworokąt ma dwie przekątne. Suma kątów w czworkącie wynosi 360
o
Wśród czworokątów można wyróżnić m.in.:
- trapezy,
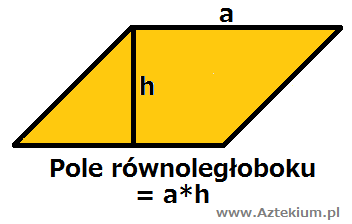
- równoległoboki,
- prostokąty,
- deltoidy,
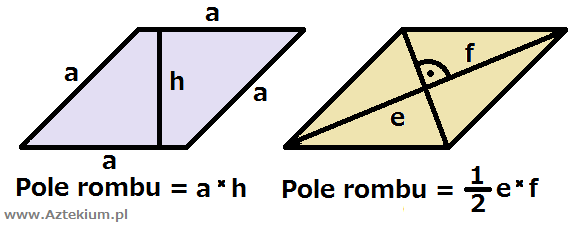
- romby,
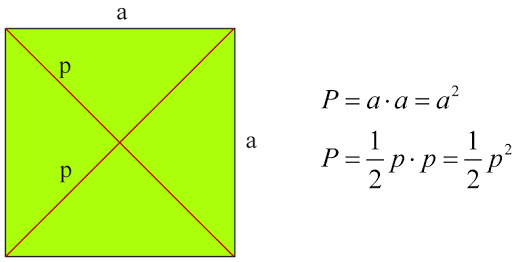
- kwadraty(czyli czworokąty foremne) .
Trapez – czworokątwypukły) mający przynajmniej jedną parę równoległych boków; (wybraną) parę boków równoległych nazywa się
podstawami, pozostałe boki noszą nazwę
ramion, odległość między podstawami nazywa się
wysokością trapezu. Niektóre potoczne definicje określają trapez jako czworokąt mający tylko jedną parę boków równoległych i zgodnie z nimi równoległobok nie jest trapezem
Równoległobok – czworokąt mający dwie pary równoległych boków. Równoległobok jest szczególnym przypadkiemtrapezu. Jego przeciwległe boki są nie tylko równoległe, ale też równej długości. Jegoprzekątne przecinają się w połowie swojej długości (nie zawsze pod kątem prostym). Przeciwległe kąty są równej miary. Suma miar kątów sąsiednich, czyli leżących przy tym samym boku, wynosi 180° .
Romb (rzadziej ukośnik) – czworokąt o bokach równej długości. Każdy romb jest równoległobokiem, którego boki mają tę samą długość, i jednocześnie jest deltoidem, którego przekątne przecinają się w swoich środkach. Szczególnym przypadkiem rombu jest kwadrat, który jest rombem o kątach prostych i jednocześnie jest rombem o przekątnych tej samej długości
Prostokąt – czworokąt, który ma wszystkie wewnętrzne kąty proste (stąd również jego nazwa). Prostokąt jest szczególnym przypadkiem trapezu prostokątnego oraz równoległoboku. Szczególnym przypadkiem prostokąta (o wszystkich bokach tej samej długości) jest kwadrat.
Prostokąt, który nie jest kwadratem, ma dokładnie dwie osie symetrii i środek symetrii. Przekątne prostokąta są równej długości i przecinają się w połowie. Kąt między przekątnymi jest prosty wtedy i tylko wtedy, gdy prostokąt jest kwadratem.
Kwadrat (
quadratum czworobok, kwadrat) o czterech bokach (czworokąt foremny), czyli czworobok o czterech przystających bokach (a stąd równej długości) i tyluż przystających kątach wewnętrznych (a stąd prostych). Można go również scharakteryzować jako prostokąt o przystających bokach (bądź równej długości, bądź też prostokąt równoboczny), romb o przystających (bądź prostych) kątach wewnętrznych. Dowolne dwa kwadraty są podobne.
Sześciokąt foremny
Twierdzenie Pitagorasa
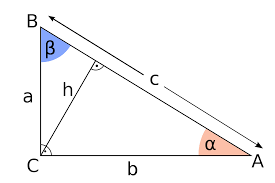
W dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta. Zgodnie z oznaczeniami na rysunku obok zachodzi tożsamość
a2 + b2 = c2
Geometrycznie oznacza to, że jeżeli na bokach trójkąta prostokątnego zbudujemy kwadraty, to suma pól kwadratów zbudowanych na przyprostokątnych tego trójkąta będzie równa polu kwadratu zbudowanego na przeciwprostokątnej.
Odkrycia dokonali Babilończycy, którzy znali dodatkowo dwie prostsze metody, przy których błąd jest niewielki. Zapewne znali je przed Pitagorasem starożytni Egipcjanie. Wiadomo też, że jeszcze przed nim znano je w starożytnych Chinach i Indiach.
Twierdzenie odwrotne
Jeżeli suma kwadratów dwóch krótszych boków w trójkącie jest równa kwadratowi najdłuższego boku to ten trójkąt jest prostokątny.
Twierdzenie Talesa
Jeżeli ramiona kąta płaskiego przecinają dwie proste równoległe, to odcinki wyznaczone przez te proste
na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na
drugim ramieniu kąta.
Twierdzenie odwrotne.
Jeżeli odcinki wyznaczone przez dwie proste na jednym z ramion kąta są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta, to te proste są równoległe
Koło, okrąg liczba π
Koło jest to zbiór punktów płaszczyzny, których odległość od środka koła jest mniejsza bądź równa promieniowi r. Na rysunku koło stanowi zaznaczony na czarno okrąg i błękitne wnętrze tego okręgu.
Okrąg jest to zbiór punktów płaszczyzny równo odległych od jednego punktu, czyli środka okręgu. Możemy powiedzieć językiem potocznym , że jest to „obrączka”, a na rysunku okrąg o środku O i promieniu r został narysowany czarnym kolorem.
Promień to odległość między środkiem okręgu koła, a jego brzegiem.
r – to oznaczenie promienia.
Liczba π (PI)
Stosunek obwodu koła do jego średnicy jest liczbą stałą oznaczaną symbolem π (czytaj: pi) równą w przybliżeniu 3,14.
Liczba Pi (π) jest to liczba niewymierna tzn. Pi nie ma skończonego lub okresowego rozwinięcia dziesiętnego.
Rozwiniecie dziesiętne liczby Pi do dziesiątego miejsca po przecinku:
π ≈ 3,14159 26535 89793 23846 26433 83279 …
Rozwiniecie dziesiętne liczby Pi jest nieskończone, a w obliczeniach stosuje się tylko pewne jej przybliżenia.
Zaokrąglenia liczby π:
π ≈ 3 przybliżenie stosowane w uproszczonych zadaniach
π≈ 3,14 najczęściej stosowane w zadaniach rozwinięcie dziesiętne
π≈22/7
π≈355/113