Bryły obrotowe Janusza Wchowicza

Bryły obrotowe

Bryła obrotowa - to bryła geometryczna ograniczona powierzchnią powstałą w wyniku obrotu figury płaskiej dookoła prostej (nazywanej osią obrotu).

walec kołowy prosty,
stożek,
kula,
torus,
beczka,
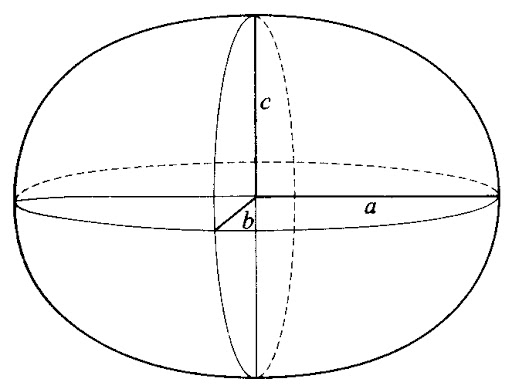
elipsoida obrotowa,
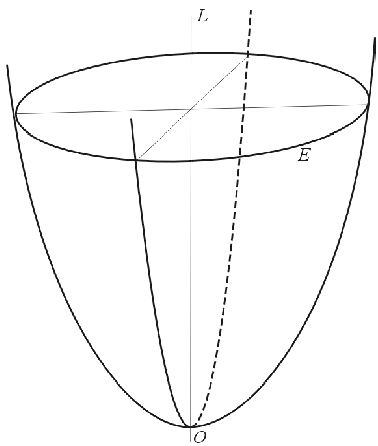
paraboloida obrotowa,
hiperboloida obrotowa.

Tak powstają bryły obrotowe

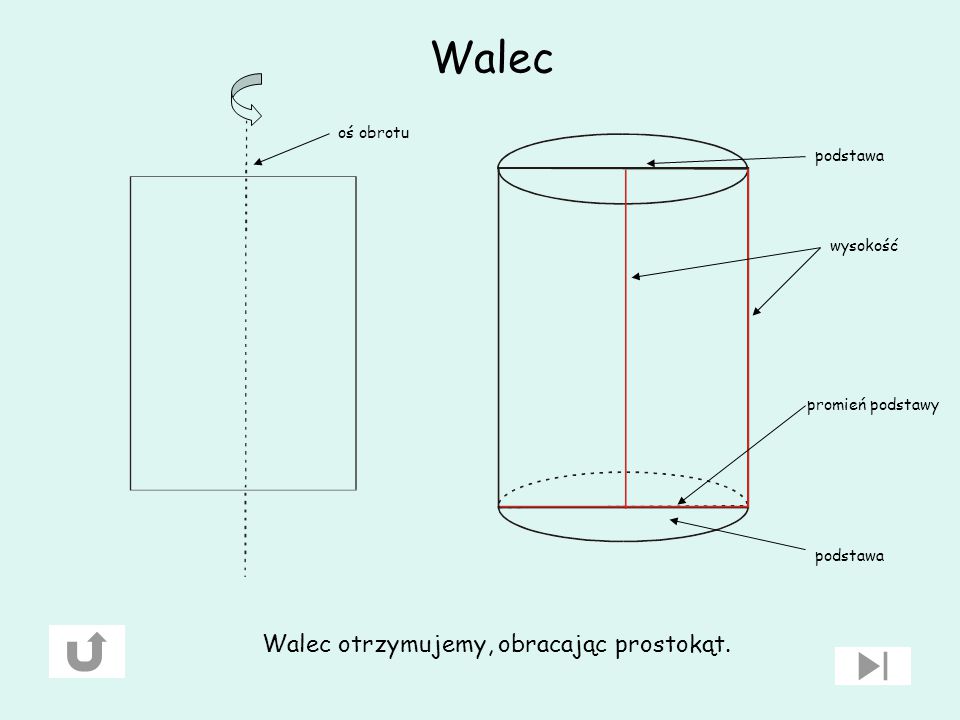
Walec

Walec kołowy prosty jest bryłą geometryczną powstałą w wyniku obrotu prostokąta wokół jednego z jego boków. Podstawą walca oraz jego górną częścią jest koło, a jego szerokość jest w każdym miejscu taka sama. – jego wysokością.
Walec jest bryłą geometryczną ograniczoną powierzchnią walcową i dwiema płaszczyznami nierównoległymi do jej tworzącej. Jeżeli płaszczyzny są prostopadłe do tworzącej, wówczas jest to walec prosty.
Walec kołowy prosty jest bryłą geometryczną powstałą w wyniku obrotu prostokąta wokół jednego z jego boków. Podstawą walca oraz jego górną częścią jest koło, a jego szerokość jest w każdym miejscu taka sama.
Walcami określa się również inne bryły i powierzchnie, których podstawą może być jakakolwiek figura płaska. Najczęściej rozpatruje się przypadek, kiedy tą podstawą jest krzywa stożkowa: elipsa, hiperbola, lub parabola.
Mówimy wówczas odpowiednio o walcu eliptycznym, hiperbolicznym i parabolicznym, przy czym jedynie pierwszy z nich może stanowić bryłę, a pozostałe dwa są powierzchniami nieskończonymi.

Opis walca

Opis walca

Wzory na walec

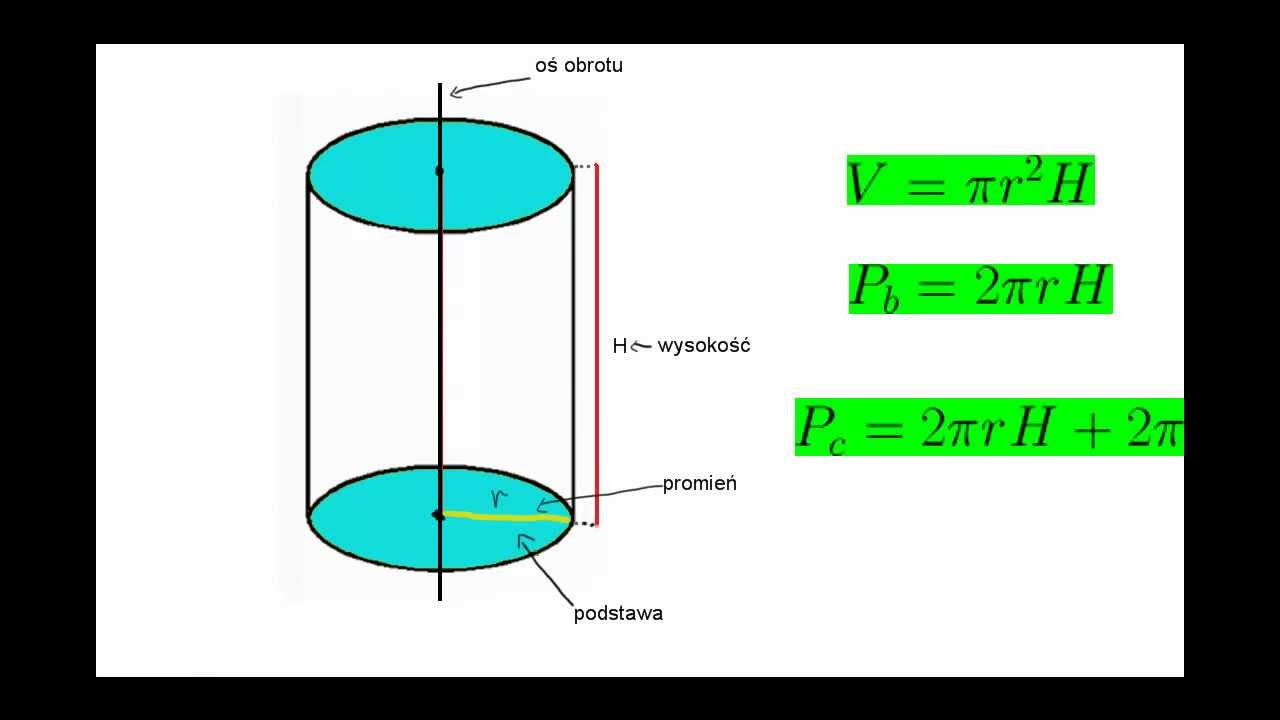
Wzory na walec

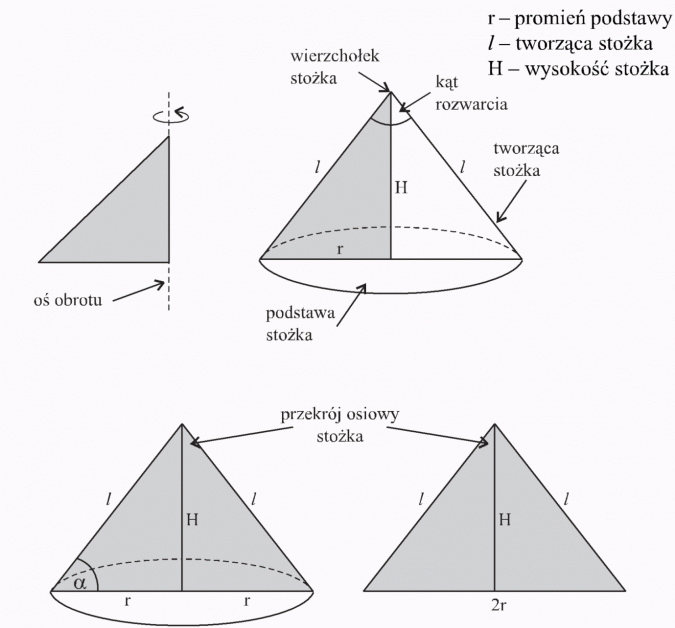
Stożek

Stożek to bryła przestrzenna powstała przez obrót trójkąta prostokątnego wokół jednej z przyprostokątnych.
Stożek (łac. conus) – bryła ograniczona przez powierzchnię stożkową, której krzywa kierująca jest zamknięta, oraz przez płaszczyznę przecinającą powierzchnię stożkową.
Część płaszczyzny wycięta przez powierzchnię stożkową stanowi podstawę stożka. Może mieć ona kształt dowolnej figury płaskiej. Kierującą powierzchni stożkowej może być obwód podstawy. Wysokością stożka nazywamy odległość wierzchołka od płaszczyzny podstawy.

Opis stożka

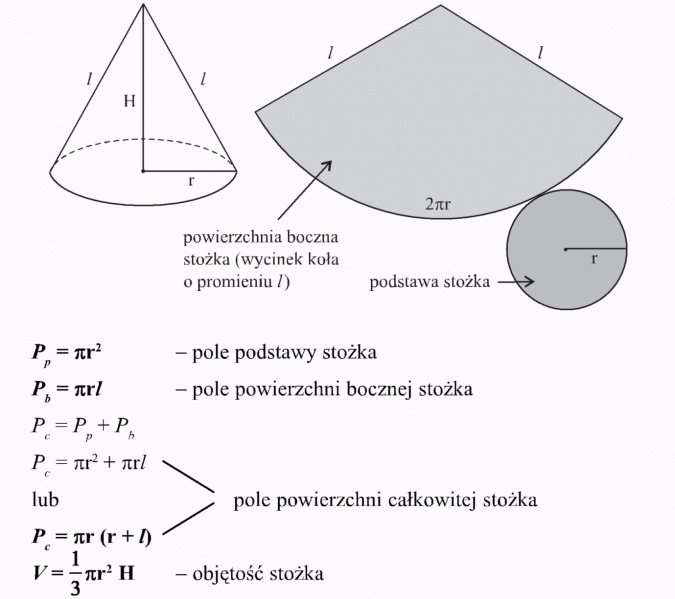
Wzory na stożek

Opis stożka

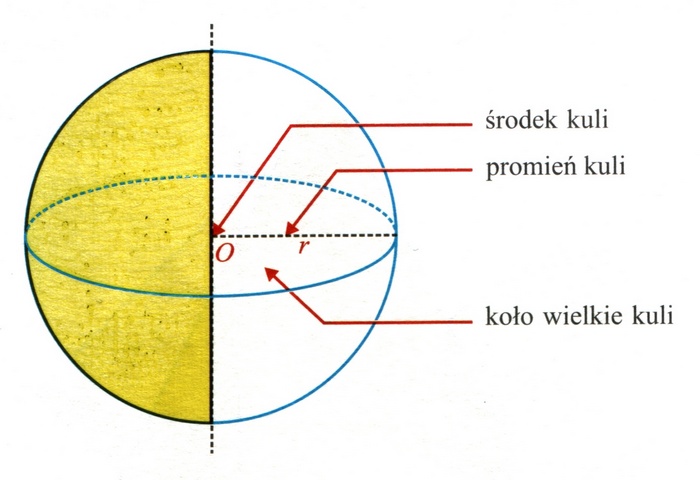
Kula

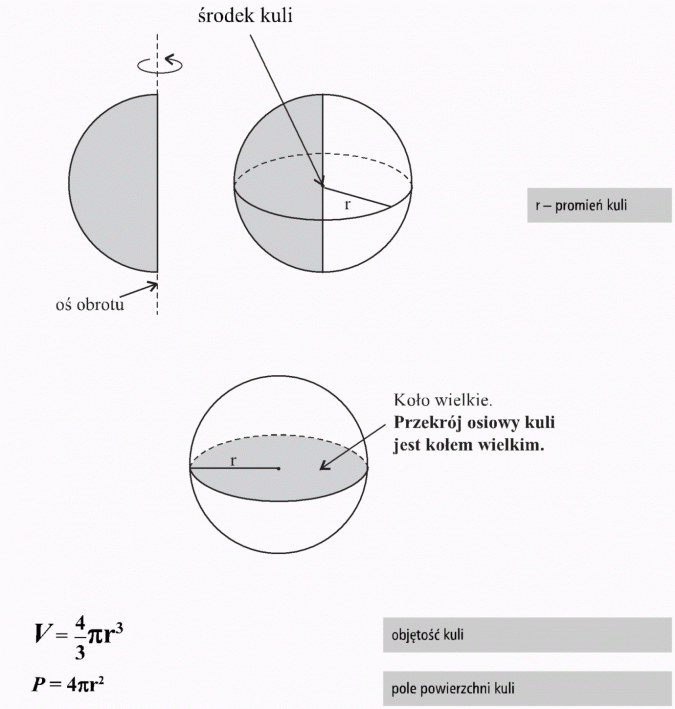
Zbiór punktów przestrzeni, których odległość od ustalonego punktu O (zwanego środkiem kuli) jest mniejsza lub równa stałej liczbie R (zwanej promieniem kuli);
Kula to bryła obrotowa, która powstaje przez obrót koła wokół osi zawartej w płaszczyźnie koła, do której należy środek koła.
Sfera jest to brzeg kuli, czyli powierzchnia powstała w wyniku obrotu półokręgu dookoła prostej zawierającej jego średnicę.
Odcinkiem kuli nazywamy część wspólną kuli i domkniętej półprzestrzeni wyznaczonej przez dowolną płaszczyznę przecinającą kulę.
Czaszą kuli nazywamy część wspólną sfery i domkniętej półprzestrzeni wyznaczonej przez dowolną płaszczyznę przecinającą kulę.
Podstawą odcinka kuli jest koło o promieniu długości .
Wysokość odcinka kuli jest to odcinek prostopadły do promienia podstawy i taki, którego jeden koniec pokrywa się ze środkiem podstawy, zaś drugi leży na sferze.
Wycinkiem kuli nazywamy sumę odcinka kuli i stożka, którego podstawą jest podstawa odcinka kuli, a wierzchołek pokrywa się ze środkiem kuli.

Historia poglądów na kształt Ziemi

Zarówno Sumerowie (4500-1531 p.n.e.), jak i Babilończycy (2000-539 p.n.e.) byli przekonani, że jest ona płaska, a pogląd ten przetrwał prawie do końca średniowiecza. W okresie rozkwitu kultury antycznej zagadnieniem tym zajmowali się najświatlejsi ludzie epoki.
Ilu jednak było myślicieli, tyle poglądów. W IX wieku p.n.e. Homer twierdził, podobnie jak Babilończycy, że Ziemia jest płaska i do tego podpiera niebo. Wielki matematyk Tales z Miletu (624-547 p.n.e.) wyobrażał sobie naszą planetę jako płytę pływającą po oceanie. Dla współczesnego mu Anaksymandra Ziemia również była płaska i usytuowana w środku wszechświata.
Dopiero słynny filozof i matematyk Pitagoras (ok. 570-495 p.n.e.) stwierdził, że ma kształt sfery. Według jego filozoficznej teorii kosmos składał się z kryształowych kul, które obracały się wokół globu wraz z zawartymi w nich gwiazdami i planetami. Dla Arystotelesa (384-322 p.n.e.) Ziemia także była centrum kosmosu, a dowodem na jej kulistość miał być kształt cienia rzucanego na Księżyc oraz zmiana wysokości gwiazd przy ich obserwacji z różnych równoleżników.
Z kolei Eudoksos z Knidu (IV p.n.e.) wysunął inny - słuszny skądinąd - pogląd, że Ziemia obraca się wokół własnej osi.
Archimedes (ok. 287-212 p.n.e.) obliczył, że jej obwód ma ok. 48 tys. km. Arystarch z Samos (ok. 320-250 p.n.e.), który jako pierwszy zasugerował heliocentryczny model świata, pokusił się nawet o określenie dystansu dzielącego Ziemię od Słońca i Księżyca. Twierdził też, że Słońce znajduje się 19 razy dalej od naszej planety niż Księżyc.
Za niezwykle istotne w rozwoju geodezji uważa się wyznaczenie wymiarów Ziemi przez żyjącego w III w. p.n.e. matematyka i filozofa Eratostenesa z Cyreny (ok. 275-194 p.n.e.). W egipskiej Syenie (obecnie Sawfana) zaobserwował on, że w czasie zrównania dnia z nocą tyczka wbita pionowo w ziemię nie rzuca cienia. Zaglądając w południe do studni; sprawdził, że promienie biegły prosto na jej dno. Wywnioskował zatem, że jeśli ustawi drugą tyczkę w innym miejscu południka i w południe (tego samego dnia roku) rzuci ona cień, będzie to dowód na to, że Ziemia nie jest płaska, lecz kulista. Jako matematyk wiedział, że do obliczenia jej obwodu wystarczy tylko zmierzyć długość tego cienia i odległość między tyczkami. Za taką "tyczkę" posłużyła mu kolumna w Aleksandrii oddalonej (według niego) o prawie 800 kilometrów od Sawfany. Na tej podstawie obliczył, że obwód Ziemi wynosi 250 tys. stadiów. W zależności od przyjętej wielkości tej jednostki (ok. 157 lub 185 m) otrzymany rezultat waha się pomiędzy 39,3 a 46,6 tys. km. Wynik jest zatem bardzo dokładny, biorąc pod uwagę niedoskonałe metody pomiaru oraz przyjęcie błędnych założeń. Sądzić jednak należy, że błędy popełnione przez Eratostenesa skompensowały się (oba miasta nie leżą na jednym południku - różnica wynosi ponad 3°, Sawfana nie znajduje się - na istotnym dla założeń - Zwrotniku Raka, a odległość między miastami, którą uczony określił na podstawie czasu przejścia karawany, wynosi tylko 725 km). Innym dokonaniem Eratostenesa było obliczenie dystansu dzielącego nas od Słońca (804 mln stadiów) i Księżyca (780 tys.) oraz kąta nachylenia płaszczyzny równika do ekliptyki (23°51'15'').
Na sferyczny kształt planety wskazywały także doświadczenia żeglarzy, którzy dawno zauważyli, że podczas zbliżania się do portu zza horyzontu wyłania się coraz większy fragment lądu. Utwierdzały ich w tym także obserwacje gwiazd. Na ich podstawie Posidoniusz z Apamei w II w. p.n.e. obliczył, że obwód planety ma 180 tys. stadiów.
Trzysta lat później, już w czasach nowożytnych, wielki grecki astronom i matematyk Klaudiusz Ptolemeusz (ok. 85-165) w dziele "Almagest" przedstawił teorię ruchów planet w układzie geocentrycznym. Według niej planety poruszają się wokół Ziemi po skomplikowanych orbitach zbliżonych do kołowych (epicykle, deferenty), każda we własnej "sferze", a obwód globu wynosi ok. 18 tys. km.
Poglądy Ptolemeusza i jego wizja świata dotrwały aż do czasów Kopernika i wyznaczały nie tylko geodezyjne czy kartograficzne standardy. Przypuszcza się np., że Krzysztof Kolumb na podstawie mapy świata Ptolemeusza ocenił, że Azja znajduje się tylko 3-4 tys. mil morskich od Europy. Pojawianie się nowych teorii nie oznaczało jednak, że myśl o płaskim kształcie planety znikła na dobre. Przekonani co do tego byli m.in. św. Cyryl z Jerozolimy (315-386 n.e.) i Diodorus z Tarsus (?-ok. 392 n.e.).
W 1543 r. w księdze zatytułowanej "O obrotach sfer niebieskich" wielki polski astronom Mikołaj Kopernik (1473-1543) opisał nowy heliocentryczny model Układu Słonecznego. W jego środku znajdowało się Słońce, a nasza planeta wraz z innymi obiegała je po kołowych orbitach. Ziemia była oczywiście kulą, a wokół Słońca krążyła wraz z obiegającym ją Księżycem. Był to pogląd rewolucyjny i podważający obowiązującą dotąd wizję świata ptolemeuszowskiego. I chociaż z uwagi na niedoskonałość ówczesnych instrumentów astronomicznych Kopernik nie był w stanie w pełni udowodnić swojej teorii, to jest bezsporne, że dała ona podstawy do dalszego rozwoju nauk ścisłych: do prac Galileusza, Keplera, Newtona i innych.
Niespełna sto lat po śmierci Kopernika jego poglądy potwierdził włoski astronom, fizyk i filozof Galileusz, Galileo Galilei (1564-1642), który jako pierwszy wykorzystał lunetę do prowadzenia pomiarów astronomicznych. Jak się wkrótce okazało, nowy instrument oddał nieocenione usługi nie tylko w astronomii, ale i w geodezji. Luneta pozwoliła Galileuszowi zobaczyć plamy na Słońcu, dzięki czemu wyznaczył okres obrotu naszej gwiazdy. Z kolei wnioski wysnute na podstawie obserwacji faz Wenus były dla niego potwierdzeniem teorii głoszonej przez Kopernika. W rozprawie pt. "Dialog o dwu najważniejszych układach świata: ptolemeuszowskim i kopernikańskim" Galileusz zawarł uzasadnienie teorii heliocentrycznej. Mimo to zarówno dzieła Kopernika, jak i Galileusza przez długi czas były na papieskim indeksie ksiąg zakazanych (oficjalnie zostały z niego usunięte dopiero na początku XIX wieku). W Kościele jeszcze przez kilka stuleci obowiązywał bowiem model świata Ptolemeusza.
Rację, jak wiadomo, mieli Pitagoras i Kopernik, ale wnioski wysnute na podstawie obserwacji astronomicznych czy traktatów filozoficznych czekały na potwierdzenie z pomiarów samej planety. Oprac. Jerzy Przywara